一張數理邏輯海報
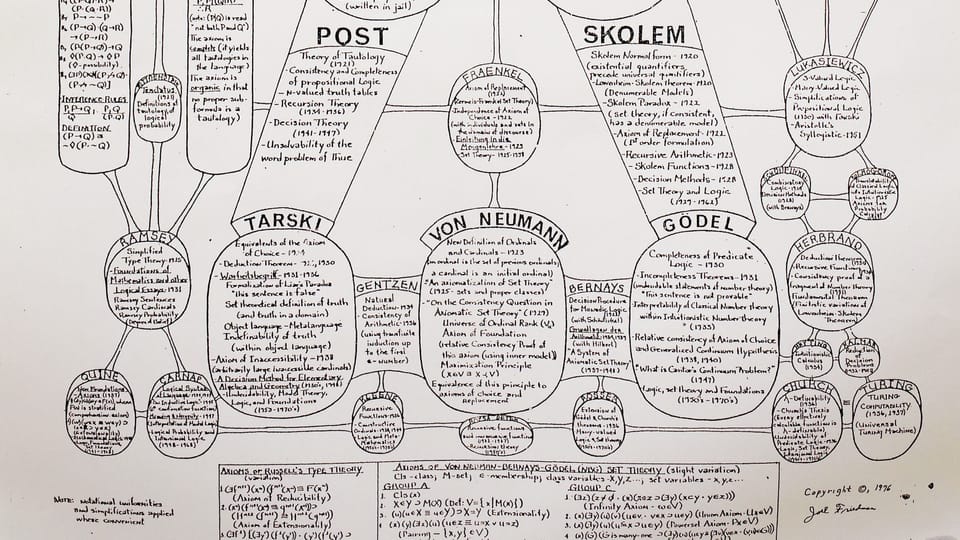
找舊照片時看到這張十年前(2014年拍攝)的照片,既然網站可以放原圖出來而不會被壓縮,便貼出來留個記錄(剪裁了邊緣和修正了顏色)︰
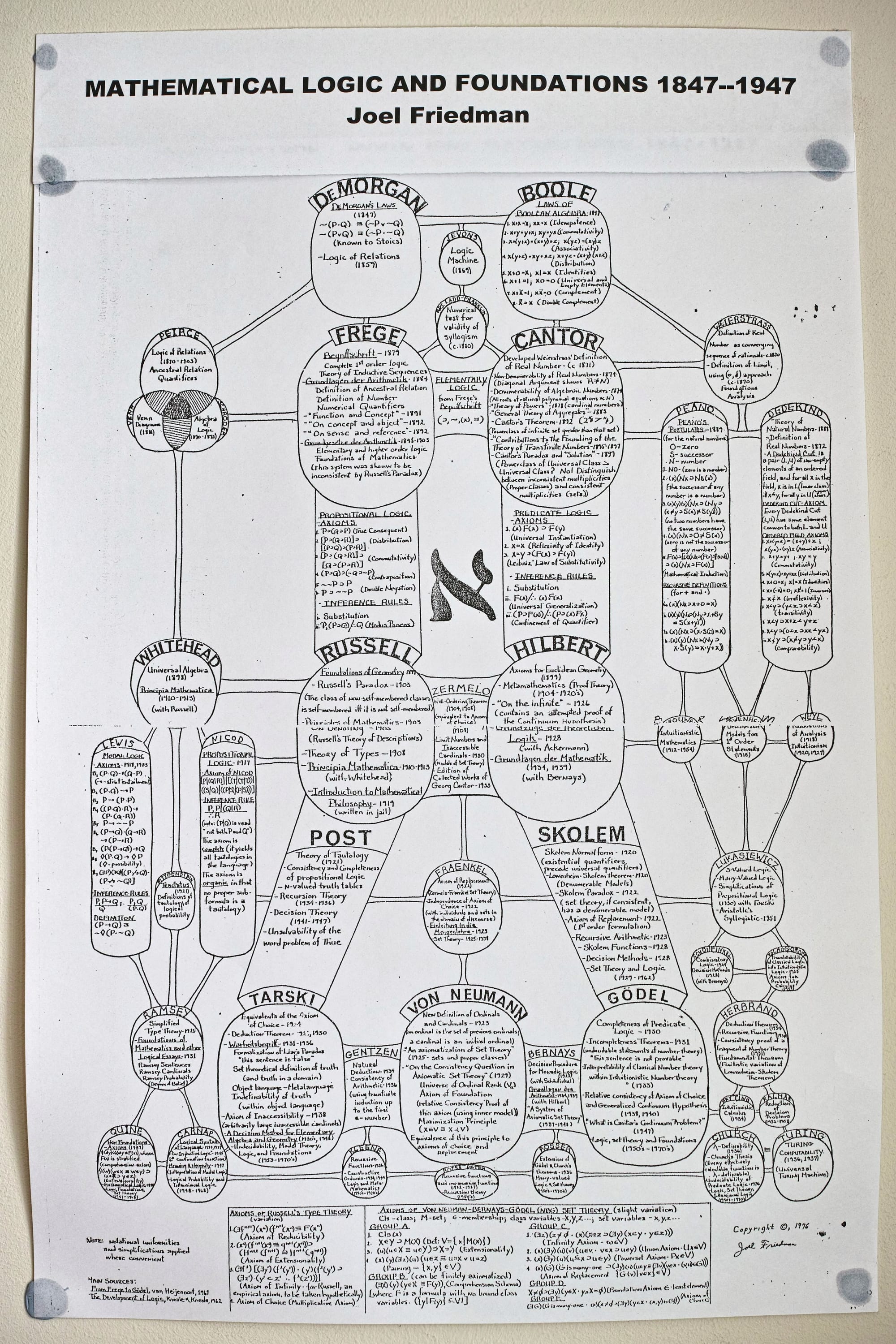
(2024-07-04 更新︰發現拍了另一張更清晰的照片,所以換了。)
這張海報在我讀碩士的匈牙利羅蘭大學(Eötvös Loránd University, ELTE 註)邏輯學系,圖中介紹1847至1947年間多位數學家、邏輯學家及哲學家的貢獻,這段期間數理邏輯及數學基礎研究高速發展。
由於不想純貼照片而寫點東西,查了才發現同一張海報於2014年也上了Daily Nous。
南卡羅萊納大學(University of South Carolina)哲學系教授Justin Weinberg表示系上一張海報自任何人有記憶以來都存在,猜測署名的 Joel Friedman 為加州大學戴維斯分校(UC Davis)的榮休哲學教授,於是拍了張照片及投稿Daily Nous希望得到更多消息。文章刊出後Weinberg收到電郵表示普渡大學(Purdue University)也有同一海報,Friedman更親自電郵解說海報背景,詳情可參考該文︰

我較感興趣的是Friedman提到他博士論文是關於一套叫STC (“the set theory of proper classes”) 的集合論,他畢業後不久便轉向研究其他哲學領域,但我查到他留下了一篇相關論文(相信改寫自其畢業論文)。
在Sci-Hub找了這篇論文速讀,發現當中提到 Arnold Oberschelp 1964年的論文,我讀碩士時其中一科介紹另類集合論(Alternative Set Theory)的老師曾提到這篇論文,說他那一套集合論中容許把proper class當成urelement去處理,這個奇特想法令我留下印象(我還查得到自己儲存這篇論文的日期︰2014-01-17)。Oberschelp的論文是德語,我看不懂,雖然他有另一篇Set Theory over Classes用英語,但我還是未讀。
在集合論中,urelement是指那些並非集合但可以屬於某個集合的物件,又稱作atom或individual。沒有urelement存在的集合論稱為pure set theory,現時屬集合論主流,所有集合都是透過空集發展出來,但urelement在集合論發展早期頗為常見。
樸素集合論(Naive set theory)隱含不少矛盾,後來公理化集論合的發展旨在消除這些悖論,一個常見限制是不容許「所有集合的集合」(或稱為universal set)存在(有些理論如Quine的New Foundation容許universal set存在),可是這些理論都在描述集合,那麼所有集合組成的整體是甚麼呢?
有些理論基本上不談(例如主流的ZFC),只證明不存在包含所有集合的集合。有些理論(如NBG,見上圖最底)則假設class(譯作「類」)存在,定義集合為「可以屬於另一個類的類」。在這種理論中,「所有集合的類」(常稱為V)並不構成矛盾,但它不能屬於另一個類(否則就變成集合而產生矛盾),這種「不是集合的類」就稱之為proper class。那proper class到底是甚麼呢?一種常見觀點為「proper class是那些大到不能成為集合的東西」,更準確的說法是「那些能夠跟V一一對應的都是proper class」。
從這個角度看urelement和proper class處於集合論的兩端,兩者都不是集合,但前者是最基礎、構成集合的東西,後者是由極大量集合所構成、大到難以處理的東西。正因如此「把proper class當成urelement」的處理方式就顯得有趣,就像「整個宇宙其實是個subatomic particle」的科幻小說構思,或是 Rudy Rucker 在 Infinity and the Mind 提及的circular scale(12年前讀此書時對集合論了解還不夠深入,應該重讀)。當然這個理論中的proper class跟上述的proper class有顯著分別(因為NBG的proper class不能屬於其他類),詳情則留待我慢慢理解。
最後放張校園貓照,我就讀的邏輯系就在左邊大樓︰

註︰大學名字自然與演員羅蘭無關,是為了紀念物理學家Eötvös Loránd,中文《維基百科》譯作「厄特沃什·羅蘭」,又提到中文常稱厄缶(音否)。匈牙利人習慣先姓後名(寫英文時會反過來),所以Eötvös才是姓氏,ELTE其實應譯作「厄缶大學」。