接受構造主義數學的五個階段

注意︰本文跟數學哲學中的構造主義有關，並非討論數學的教學方法。

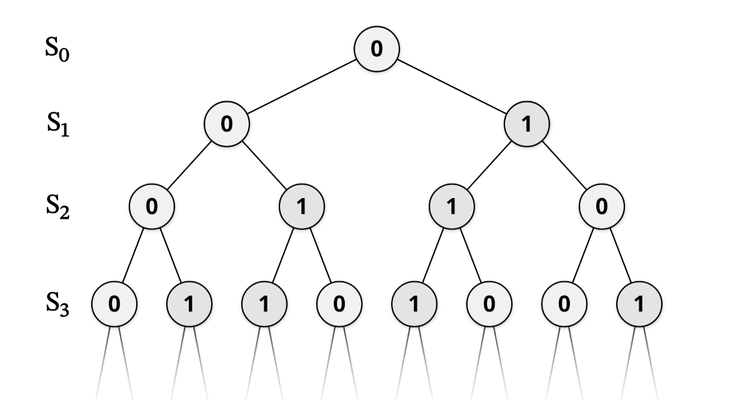
數學家 Andrej Bauer 去年為普林斯頓高等研究所（IAS）演講，主題是「Five Stages of Accepting Constructive Mathematics」，他參考著名的 Kübler-Ross 模型，把原本面對死亡的五個階段——否認、憤怒、討價還價、抑鬱和接受——改為接受構造主義數學的五個階段。

Bauer 亦把演講內容寫成文章，可在網上讀到（連結見文末）。

構造主義（constructivism）是數學哲學的一個流派，強調要證明某數學物件存在，必須能夠提供找到它的方法，或者解釋如何構造它。因此，經典數學中以反證法證明某數學物件存在——假設其不存在，推導出矛盾——從構造主義角度看並不成立。

構造主義數學（constructive mathematics）就是從符合構造主義的數學。需要留意的是，構造主義數學不只一種，L. E. J. Brouwer 的直覺主義數學、A. A. Markov 的遞歸數學等。

傳統上對構造主義數學的一大批評，在於「綁手綁腳」，嚴重限制數學家可用的工具，當中最為顯著的例子就是排中律。文中引述數學家 Michael Beeson 的評論，指 Erret Bishop 在 1967 年出版的 Foundations of Constructive Analysis 顯示了，認真對待構造主義數學，不必然要放棄現代數學的重要部份。

當然，放棄排中律仍然會導致一些看來違反直覺 — — 至少是受經典數學訓練下產生的直覺——的結果，例如，排中律跟以下陳述等價︰有限集的子集都是有限集。

不過經典數學中也不是沒有違反數學的結果，例如接受選擇公理的話，就必須接受 Banach–Tarski 悖論。選擇公理亦蘊涵排中律，換言之要放棄排中律，就得連選擇公理一併放棄。

文中一些證明顯示，有時候採用構造主義數學，可以使人辨認出對證明所用假設（正如選擇公理當年引起爭議，令人發現原來不少證明早已暗中使用此公理），增加對數學的理解。

而且剔出排中律後的構造主義數學，可以看成是經典數學的推廣，Bauer 甚至反過來說，指以經典數學的視角看構造主義數學，就像透過阿貝爾群（abelian group）來研究非交換代數（noncommutative algebra）。

至於整篇文中我認為最有說服力之處，在於提到當代集合論領域中——拜 Paul Cohen 的力迫法（Forcing）所賜——數學家研究的數學世界根本不只一個，而是「多重（集合論）宇宙」。還在嘗試劃下界線區分「經典數學」和「構造主義數學」兩個世界？Cantor 的天堂已分裂成無數個宇宙了。

然而這是從（數學）多元主義的角度去支持構造主義數學，相信跟大部份構造主義者的立場有別。無論如何，文中一些構造主義證明的例子頗有趣。

Bauer 的文章︰Five stages of accepting constructive mathematics

（原文見Medium）