未睇嘅書：The Mathematics of Logic

📕 The Mathematics of Logic: A guide to completeness theorems and their applications｜Richard Kaye*

（2025-05-06 更新：已經睇咗）

睇過 Sadie Kaye* 另一本 Models of Peano Arithmetic，Oxford Logic Guides系列，好嘢嚟。佢本人都主要研究 Nonstandard Models——Peano Arithmetic 係只包括加法、乘法同數學歸納法嘅算術系統，基於一階理論嘅限制，可以砌一啲入面包含某種大於任何「標準」自然數嘅元素嘅 models，就叫做「非標準模型」。（喺呢啲models入面用PA係區分唔到「非標準」同「標準」嘅數字。）

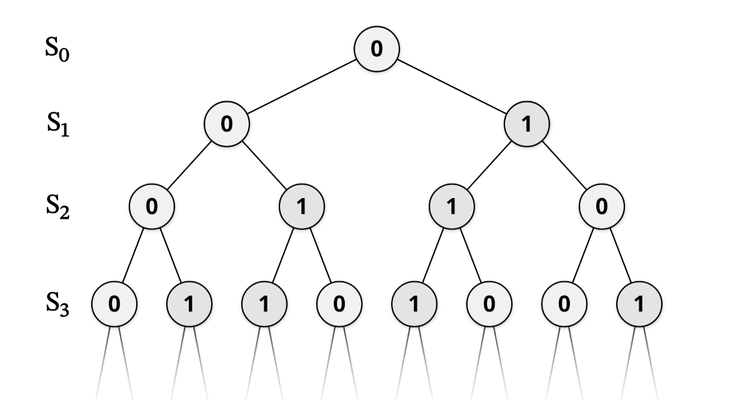
呢本書個封面係 indicate 緊 full binary tree，每一點都分兩個分支出嚟，直到永遠（所以唔可能畫晒）。呢張圖同 Kőnig's lemma 有關，條 lemma 比較弱嘅版本講緊binary tree。（Btw "Kőnig" 成日俾人寫做 "König"，佢係匈牙利人，個名入面係帶兩撇嘅 "ő" 而唔係帶兩點嘅 "ö"。）

直觀上大家應該明咩係樹狀圖，圖論入面嘅定義係由任何一點出發，點行都唔可能返返去原點（唔畀返轉頭，完全唔郁唔計），但總有方法行到去其餘嘅點。而 binary tree 就係每一點最多都只會分兩個分支出嚟嘅樹狀圖。呢個版本嘅 Kőnig's lemma 就講緊對於無限多點嘅 binary tree，總會有一條無限長嘅 path。

呢個弱化版嘅 Kőnig's lemma 對 reverse mathematics 幾重要（有個系統就以 Weak Kőnig's lemma 命名），可以理解為佢係一種弱化版嘅選擇公理。Reverse mathematics 係研究喺數學入面用乜嘢公理系統可以「剛剛好」（少一條公理都唔得）證明某啲重要定理，通常都係研究數學分析（analysis）但用二階算術處理），因為傳統嘅analysis入面好多定理都唔係constructive，可以當係睇下個系統減到幾弱而仲證明到啲有用嘅定理。

關於 reverse mathematics 嘅介紹可以睇 John Stillwell 本 Reverse Mathematics，之前寫過篇〈數學的逆向工程〉講過下本書。（Btw 篇文最尾提到三個 typos 我有 send 返 email 畀 Stillwell，佢當時話 paperback 版應該可以改返，所以要買就買 paperback。）

講返本書主題，一階邏輯嘅 Completeness theorem 本身唔算特別難，可以話係學數理邏輯嘅入門，Kaye 喺序入面提到佢唔會直接講一階邏輯，而係解釋 "a completeness theorem" 呢個數學概念（留意唔係 the，所以書名係有s），再講有咩數學應用（唔好見「應用」就以為同現實有關）。另外佢都有話好多內容係佢教大學三四年級學生嘅材料，斷估唔會太難。

* 本書作者名係 Richard Kaye，而佢喺 University of Birmingham 個網頁顯示係 Sadie Kaye 同埋 pronoun 係 She/Her。我都有諗講本書嘅作者時應該用咩名，見佢網頁顯示 publications 係用 Richard Kaye，所以最頂書嘅資料跟返，內文就用返 Sadie Kaye。

（原文見 Instagram）