《Reverse Mathematics》︰數學的逆向工程

Reverse Mathematics: Proofs from the Inside Out
John Stillwell
從有理數構造實數
在我大學一年級學過的內容當中,印象較深的不是甚麼艱深定理,而是利用等價關係,僅用自然數(及其加法、乘法)就定義出整數、有理數(及其加法、乘法),還有利用戴德金分割(Dedekind’s cut)定義出實數(及其加法、乘法)。內容並不困難,而且現在來說也不新鮮,但這是非常合我口味的數學︰用最少東西可以完成最多事情。
$\sqrt{2}$這個數字不能寫分子、分母皆為整數的分數,因此不是個有理數。我們可以找到平方越來越接近2的有理數,但就沒有一個有理數的平方為2,這樣看來有理數由小至大排列時有些「空隙」(現在我們叫這些「空隙」做無理數)。
簡單來說,戴德金分割就是把有理數集$\mathbb{Q}$「切」成符合以下條件的兩個集合$(L,R)$︰
- $L$ 及 $R$ 合起來包含了所有有理數,即$L \cup R = \mathbb{Q}$;
- $L$ 及 $R$ 都不是空集(即兩個集合都有元素);
- $L$ 內的有理數,都小於$R$的有理數。
直觀而言,就是把有理數由小至大、從左到右排列,然後切成兩份,左邊的是 $L$,右邊的是 $R$,兩個都是無限集。每個符合上述條件的 $(L,R)$ 都代表一個實數(其實只需要$L$或$R$其中一個已經足夠)。例如設$L^\ast= \{ x\in\mathbb{Q}: x^2<2 \}, R^\ast= \{ x\in\mathbb{Q}: x^2>2 \}$,那麼 $(L^\ast, R^\ast)$ 就對應 $\sqrt{2}$ 這個實數。當然,我還需要定義加法和乘法,在此不詳細說了。
戴德金這個想法,某個意義下是用「空隙」本身來填補有理數的「空隙」,從而構造出實數。
這其實是所謂「分析算術化」(arithematization of analysis)過程的一部分,從而讓微積分奠基於嚴格的實數理論之上,再層層推溯到算術(自然數及其加法、乘法)之上。就這樣,我們對數學的信心,就取決於對算術的信心。
事情當然沒有那麼簡單。
但為免加入太多技術細節,簡單來說,問題主要出於如何定義集合,或者說,我們容許甚麼集合存在。
康托定理(Cantor’s theorem)告訴我們自然數所組成的集合並不可數(uncountable),無法把它們以逐個排隊的方式列出來,因為自然數所組成的集合實在太「多」(當涉及無限,我們需要擴張「多少」的定義)。實數集同樣不可數,而且跟自然數的冪集(power set,即其元素為所有子集的集合)一一對應,我們亦可用無限的有理數集定義實數。
然而我們理論上可用的有限符號串只構成一個可數無限集,換言之仍有無限個——幾乎是所有——實數無法定義。如果我們接受任意的集合,問題當然不大,不過有些數學家基於哲學上的理由,不接受無法定義的集合,甚至只接受可計算的集合。
假如透過限制公理去減少可使用的集合,就會影響到模型內有甚麼實數存在,也限制了可以證明的定理。但到底會有甚麼影響?
逆向數學
John Stillwell 的《逆向數學》(Reverse Mathematics: Proofs from the Inside Out,筆者自行翻譯)所介紹的數學領域「逆向數學」——又有人譯作「反推數學」——就是研究這個問題。(對,寫了那麼多,其實我想介紹這本書。)
平日數學家從某個公理系統出發,去尋找、證明新定理;而逆向數學則相反,是希望尋找恰當的公理去證明新定理。怎樣才算「恰當」呢?書中引用這個領域的奠基者 Harvey Friedman 的話來說︰
當一條定理從恰當的公理證明,那些公理就能夠從該定理去證明。(When the theorem is proved from the right axioms, the axioms can be proved
from the theorem.)

在此先岔開一下話題,書中主要內容為數學,對 Friedman 著墨不多,不過他本身是個值得一寫的數學家。Friedman 在中小學跳了兩級後,參加一家大學的暑期課程,再讀到羅素(Bertrand Russell)的《數學哲學引論》(Introduction to Mathematical Philosophy),決定向數理邏輯進發。16歲的時候,他跳過大學直接進入麻省理工學院的研究院,並於18歲取得博士學位,同年成為史丹福大學助理教授。
Friedman 亦有個讀工程的妹妹(他的父親起初希望 Friedman 讀工程),後來成為 IBM 的電腦程式員,至於小他5歲的弟弟 Sy Friedman 同樣研究數理邏輯,是集合論及遞歸論的專家。
基礎理論
言歸正傳,逆向數學像逆向工程一樣,拆解已知的發現,以了解目標(定理)如何構成、有甚麼條件。而其實早於逆向數學成為一個數學領域之前,數學家已研究過類似問题。
以往很多數學家不接受歐幾里德的第五公設——下圖中,如果 $\alpha+\beta<180 ^\circ$,那麼兩條(未相交的)線將會在(向 $\alpha$ 及 $\beta$ 那邊)延長後相交——乃不證自明。
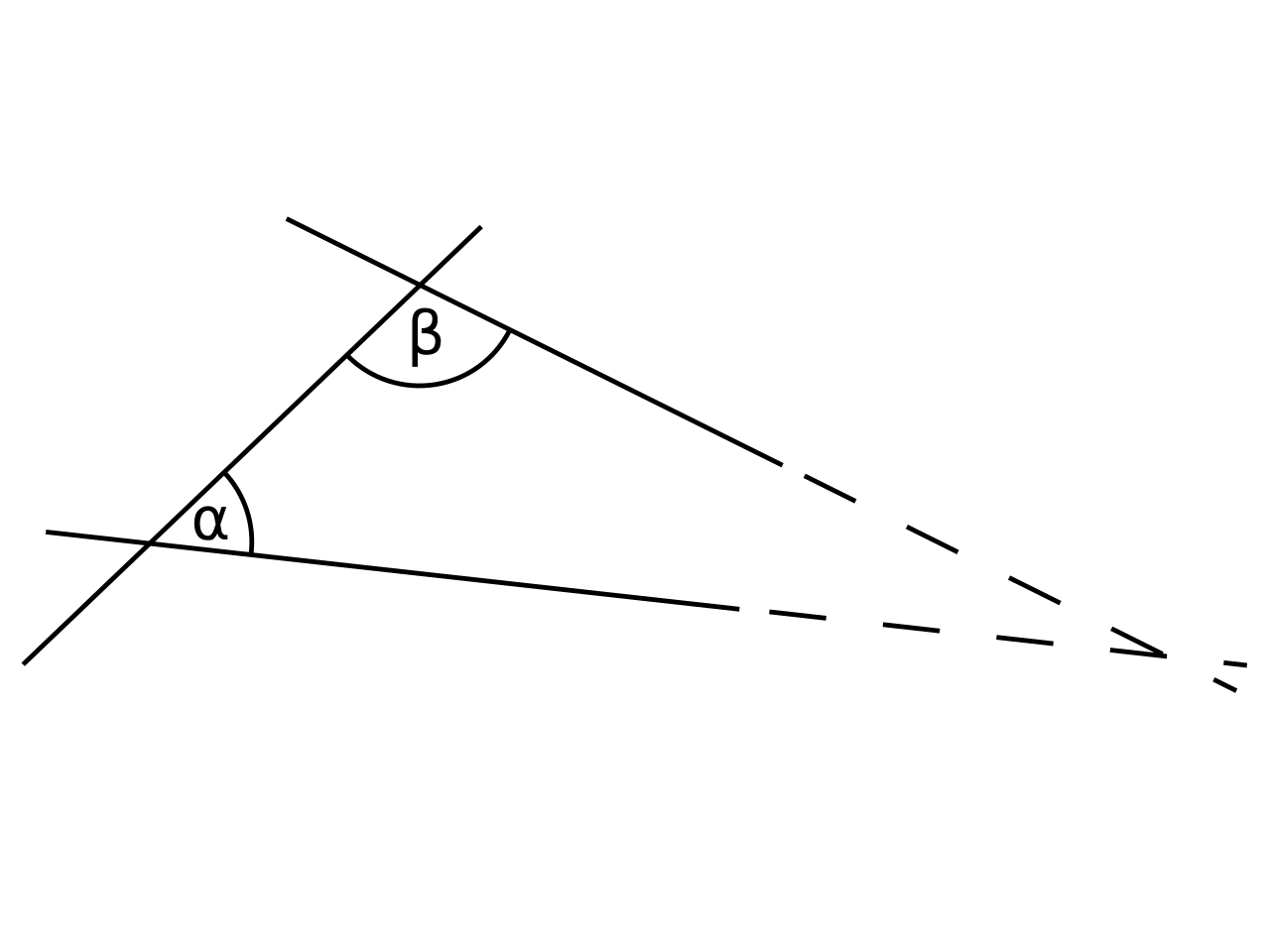
當時的數學家希望從歐幾里德其他公設證明第五公設,卻發現並不可能,更發現了非歐幾何存在。假如刪除了第五公設(而不補回任何公理),餘下的幾何系統雖然無法證明第五公設,但能夠證明它跟某些命題等價,換言之,用這些命題代替第五公設,同樣可以得出歐氏幾何。
這個較弱的理論可作為一個「基礎理論」(base theory),本身弱得無法證明太多定理,同時足夠強去證明「如果X成立,則Y亦成立」之類的命題的系統。
數學分析與可計算性理論的交集
《逆向數學》以歐氏幾何發展作簡介,不過書中主要內容並非幾何學,而是數學分析(mathematical analysis)及可計算性理論(computability theory)的交集。
作者先講述算術化的過程——即本文起首提及的內容——以及一些實數的特性,再引入皮亞諾算術(Peano Axioms)及康托定理等。然後作者介紹一些經典的數學分析定理,例如︰
- 介值定理(intermediate value theorem)︰假如函數 $f(x)$ 在區間 $[a,b]$ 之間連續,而且 $f(a)<0$ 及 $f(b)>0$,則存在某個位於 $[a,b] $之內的 c,使得f(c)=0。
- 極值定理(extreme value theorem)︰假如函數 $f(x)$ 在區間 $[a,b]$ 之間連續,則在此區間內有最大值及最少值,即存在位於 $[a,b]$ 之內的 $c$ 及 $d$,對於任何 $[a,b]$ 之內的 $x$,$f(c)<f(x)<f(d)$。
- Bolzano–Weierstrass 定理(數列版本)︰每個有界(實數)數列(bounded sequence)都有一個收斂的子數列。
假如已經把這些定理都忘掉了也不要緊,書中均有解釋及證明,相信不難重新學會。(我認為寫得淺白,但不肯定未接觸過相關內容的讀者會否覺得此書艱深。)
接下來是可計算性理論入門,作者先簡介何謂「可計算」(computable),而未有加入太多技術細節,讓讀者初步了解「可計算」和「可計算枚舉」(computably enumerable)的分別,以及跟分析學有何關係——可計算的數列可能有一個不可計算的極限、可計算的無限樹狀圖可能沒有可計算的無限路徑。
初步了解概念後,才輪到技術細節。介紹可計算性理論,少不免要講一點形式系統和圖靈機之類,作者使用史慕揚(Raymond Smullyan)的「初始形式系統」(elementary formal systems, EFS),他認為這是最簡潔的進路(我認為他沒錯)。即使如此,這些內容仍然頗為繁瑣,第一次接觸可能會迷失在符號當中,我建議如有需要不妨暫時略過。
三套系統
經過大量準備工夫後,全書的「主菜」是研究分別稱為 $RCA_0$、$WKL_0$ 及 $ACA_0$ 的系統,以及各種定理可以從哪個系統中證明。$RCA_0$ 為最弱的一個系統,只容許可計算的集合存在以及經弱化的歸納公理(induction axiom),它可證明介值定理,但書中提到的多數定理都無法證明。然而 $RCA_0$ 亦很有用,因為可用來證明 $WKL_0$ 、$ACA_0$ 的相關公理各自跟若干定理等價(兩個系統本身有分別——$WKL_0$ 比 $ACA_0$ 弱)。
另外值得一提的是 König 引理︰如果一個無限的樹狀圖中,每一節點都連上有限數目的點,則存在一條無限長的路徑。以較形象化的方式去想,就是一棵無限多分枝的樹之中,如果每條樹枝都只長出有限數量的椏枝,那麼我們可以不斷爬上去而沒有盡頭。
König 引理有個弱化版本,大致上跟 König 引理一樣,但限制每個節點只連上最多兩點(即每條樹枝最多只長出兩條分枝),看來兩條定理差別不大,然而弱化版的 WKL(weak König lemma)確實更弱——König 引理蘊涵 WKL,WKL 則無法證明 König 引理。
$WKL_0$ 系統正是加入 WKL 作為公理,可以證明到部分重要定理,但 König 引理需要在更強的 $ACA_0$ 系統中才能夠證明。$ACA_0$ 不僅可以證明所有 WKL₀ 內的定理,更能夠證明 $WKL_0$ 的一致性,根據哥德爾不完備定理(Gödel’s incompleteness theorems),除非 $WKL_0$ 本身不一致,否則 $ACA_0$ 是個比 $WKL_0$ 強的系統。
逆向數學最有趣之處不在於發現新定理,而是了解如何刪減假設,找出恰好能夠證明某條定理的公理。$RCA_0$ 的限制令到某些常用證明方法不適用,但在「綁手綁腳」下證明,倒令人可以用新角度理解,察覺到過往不自覺使用(而其實不必要)的假設,以及想當然的直觀圖像。
勘誤
最後提醒一下打算讀此書的人,需要注意書中有三個小錯誤︰
- 第40頁,關於 successor fucntion 的第二條公理, “For all $m$ and n, $S(m) \neq S(n) \Rightarrow m\neq n$” 一句有誤,當中的 “$\neq$” 應為等號(或者箭號左右兩句需要倒過來)。
- 第49頁,講述 the diagonal argument 的時候,diagonal set 應為 $X$,其中一句(“then $D$ is itself an arithmetically definable set”)誤植為 “$D$”。
- 第56頁,關於 the fundamental theorem of algebra 的部分,“for $n$ large and positive” 及 “for $n$ large and negative” 兩句中的 “$n$” 應為 “$x$”。
相關文章︰