量子電腦不（太）可能是下一代個人電腦

早前施永青寫移民，指未來「香港人可能已經習慣IoT(萬物互聯)，用量子電腦」而貽笑大方，同日在Facebook見到有個叫William Kou的帳戶一篇關於半導體的帖文，有過千次分享，作者同樣以為量子電腦是用來取代現有的晶片︰

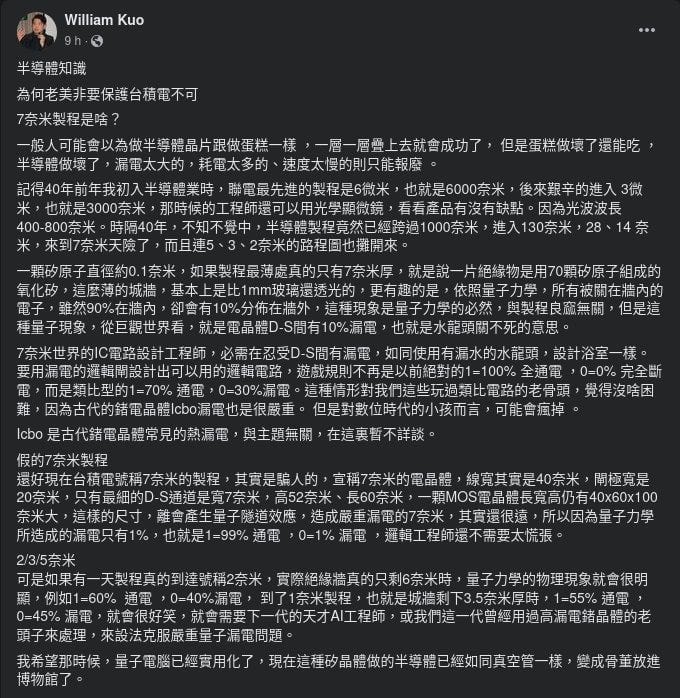
首先得指出，這篇文章是抄回來的，原文出自Rudolf Young（William Kuo事後補回連結及作者名稱，指自己「初心只是好文分享」，雖然我也不明白為何原本的帖文完全沒指出自己不是作者及附上文章來源）。

至於那篇原文單在Facebook（未計轉載）已有上萬次分享。作者看來曾在半導體產業工作，有專業背景，但還是會誤解了量子電腦（這是另一個專業）的用途。（另外他對Intel及AMD那段的評價我認為也不準確，但在此不談。）

簡單來說，當半導體晶片的製程越縮越小時，的確會如截圖文章所指般遇上量子穿隧道效應（quantum tunneling effect），但這是工程師不想見到的量子效應。至於量子電腦則相反，工程師和電腦科學家利用量子效應去運算，從而在處理特定問題時得到現時超級電腦也無法企及的效能。

當然，我自己也沒甚麼專業背景，不懂量子力學也不懂工程方面的東西，只是對計算複雜度理論（computational complexity theory）有點皮毛的理解，也因為對量子電腦有興趣而讀過一些書和文章。以下重點放在計算複雜度理論方面，至於量子電腦的原理及工程問題，坊間應有大量好文章，我就不獻醜了。

計算複雜度理論簡介

量子電腦不會成為下一代個人電腦的一大原因，在於量子電腦只擅長處理特定問題。要理解這類問題的特點，就得先了解一點計算複雜度理論。粗略來說，這是數學家、電腦科學家為問題——當然只研究可以透過計算處理的問題——難度分類的學科。問題越難，理應越需要更多時間計算，所以這門學科實際上研究「解決特定問題的最佳演算法」，但有兩點須要注意︰

1. 證明某個演算法是解決問題的最佳演算法並不容易，所以很多時都只能夠透過「已知最佳演算法」去計算上下限；
2. 電腦硬件不斷進步，所以運行演算法的速度自然越來越快，但這門學科並不研究實際上的運行時間，而是理解演算法（一般來說是在最差的情況下）須需多少次運算才可得出答案，這自然要對應特定的運算模型（例如圖靈機）。

不過第2點的說法其實也不準確。演算法的輸入數字越大，通常所須的運算就更多（除非是極簡單的演算法，或者剛好某個輸入容易得出答案），計算複雜度理論研究的是「當輸入越來越大時，演算法得出答案所須的運算次數的增長幅度」。另外，從非常基礎的角度而言，真正重要的是輸入字串長度（不同數字可以有相同長度，當然數字更大時相應字串也更長），所以再修正一下，真正要研究的是「當輸入字串越來越長時，演算法得出答案所須的運算次數的增長幅度」。

這個關係可以用函數來表達︰當輸入的字串長度為n時，某演算法最多只須要f(n)次運算便可得出答案。這個函數f為該演算法的時間複雜度（time complexity），計算複雜度理論還會研究其他類型的複雜度，但既然這是簡介就先不說太多。

假如我們已知有個演算法可以解決某個問題，而且這個演算法的時間複雜度是一個多項式，那麼這個問題就屬於稱為P的類別內。通常P內的問題都被視作容易解決。

假如我們已知有個演算法可以在多項式時間內驗證正確答案，這個問題就屬於NP這個類別。由於除法運算屬於P，「給定一個數字，尋找其因數」這問題就屬於NP——只要有正確答案（指定數字的一個因數），我們可以透過除法確認答案正確。

只要找到多項式時間的演算法，就可以證明某個問題屬於P，但要證明一個問題不屬於P就難得多——得證明對於任何解決該問題的演算法，都有足夠長的輸入使運算不能在多項式時間內完成。到底只是數學家、電腦科學家未找到適當的演算法，抑或根本沒有這個演算法，往往很難判斷，例如質數判別問題要到2002年才被證明屬於P。

而計算複雜度理論中的著名未解難題 P vs. NP 就是問兩類問題是否相等。眾多NP問題中有一類被視為「最困難」的NP問題，稱作NP-complete，只要能夠證明其中一個NP-complete的問題屬於P——即找到多項式時間的演算法——便足以證明P=NP。當然，這還是非常困難，目前未有證明也未有否證，不過這個領域的專家傾向相信P≠NP。

量子電腦的限制

量子電腦利用了量子力學的特性去進行運算，1994年數學家Peter Shor設計了一套在（設想中的）量子電腦上運行的演算法，可以在多項式時間內解決因數分解問題——此問題至今尚未被證明在P內。這項結果令量子電腦可以有效破解不少公鑰加密系統，因此引起不少興趣。

要注意的是，雖然至今仍未有在多項式時間內解決因數分解問題的演算法，但也沒有任何人能證明這個問題不屬於P。換言之，可能只是未有人找到適當和適合傳統電腦使用的演算法（這正是小說《Factor Man》的題材），Shor的演算法未能足以證明量子電腦必然比傳統電腦優勝。到了2018年，學界終於解決了這個問題，但有點技術性，有興趣的讀者可以參考《Quanta Magazine》的報導。

目前已知（設想中的）量子電腦能在多項式時間內解決一些特定問題（但不包括NP-complete問題），這些問題傳統電腦至今未有有效的多項式演算法，以致量子電腦在這方面能超越現時最強大的超級電腦。但在一般運算方面，量子電腦則遠不及已發展多年的傳統電腦方便，即使未來量子電腦有普及應用，似乎較合理的做法是使用雲瑞的量子伺服器，否則只是殺雞用牛刀。

另外，要讓量子演算法順利運行，量子電腦有很多工程上的挑戰，最主要是確保系統不會受外界環境干擾產生quamtum decoherence，否則的話系統無法停留在量子態進行運算。正因如此，現時的量子電腦均非常巨大，而且需要保持極低溫才可順利運行，也未能控制足夠多量子位元來顯示其實力。當然以往的電腦也很龐大，但要縮小傳統電腦的技術難題與縮小量子電腦有明顯分別，似乎沒有甚麼好的理由相信未來會做得到。

簡言之，不要因為看到新聞說量子電腦怎樣厲害，便以為它會取代現時所有電腦。

有興趣了解多一點量子電腦，可以以下參考計算複雜度理論及量子運算專家Scott Aaronson的影片、他為《Quanta Magazine》寫的文章以及Quanta的影片︰

（原刊於Medium）