偽亂數與 P vs. NP

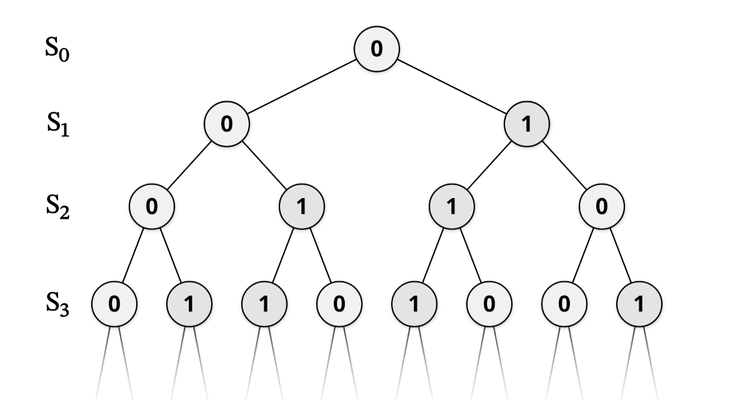
PBS Infinite Series 這一集簡介偽亂數產生器（pseudorandom number generators）——在電腦中產生「隨機」數字的演算法，由於電腦本身是非常「循規蹈矩」的東西，程式按照同一個輸入值不可能產生兩個輸出值，所以電腦最多只能產生「偽裝」隨機的數字，故名「偽亂數產生器」。

當然，正如影片中引述 Donald Knuth 的說法，偽亂數產生器的重點並非要輸出「一個」隨機的數字——這概念上有問題︰2是否「隨機」？——而是產生一連串的數字，這個序列的分佈跟隨機輸出（例如擲骰得出）的數字看來無法分辨——即通過跟隨機數列有關統計測試。

對比起使用隨機來源作為輸入值（確保結果符合隨機特性）的「真隨機」方法，偽亂數產生器仍有一些優勢，包括毋須額外硬件、較容易產生、可以複製（這在測試程式和儲存數據時有用），如非對數列有極高要求，一般情況下偽亂數產生器已經夠好。

影片簡介的內容就不再複述，在此想多說兩件跟偽亂數產生器有關的事。

偽亂數產生器其中一個重要用途，就是加密訊息。美國國家安全局（NSA）曾經力推一個稱為「Dual_EC_DRBG」的偽亂數產生器，以致美國國家標準技術研究所（NIST）亦納入其標準。但這個偽亂數產生器有一個弱點可以被 NSA 用作後門，相信是NSA推出的原因。最終 NIST 在2014年4月撤回 Dual_EC_DRBG，並建議用家盡快改用其他獲認可的演算法。

目前尚未有證明顯示，某種（嚴格）意義下——可以在多項式時間內完成，而且沒有其他多項式時間演算法可以分辨其產生的數列與隨機數列——的偽亂數產生器存在。簡單來說（反正我也不懂細節，無法說得複雜），這種偽亂數產生器存在的話，就代表單向函數（one way function）存在，反之亦然。

單向函數的特點是可以在多項式時間內計算結果，如果你知道的是輸出結果，卻無法在多項式時間內算出輸入值（即難以進行逆向工程）。如果單向函數存在，就會導致 P 不等於 NP，不過 P vs. NP 問題尚未解決，所以我們還不知道單向函數和上述偽亂數產生器是否存在。（這部分參考 Scott Aaronson 的 Quantum Computing since Democritus 一書。）

P.S. 如果你想要真正隨機生成的數值／字串，可以到 RANDOM.ORG。

（原文刊於Medium）