直覺主義、π以及排中律——《大話題︰邏輯》相關段落的問題

(按︰原文分別為一則Substack Note及Substack文章,現合併刊出)
在《泛科學》見到這篇轉載《大話題:邏輯》一書內容的文章,錯得有點離譜。

- 我少讀邏輯史,但說歸謬法是Leibniz發明未免與歷史相差太遠。古希臘時期的數學已使用反證法,例如質數有無限多個、2的平方根是無理數的證明。
- 漫畫中疑犯那句「我在打籃球,沒有去搶劫」並沒有自相矛盾,只是與醫生提供的訊息「疑犯的手臂前一天摔斷了」(及「手臂摔斷後不可能在一天內復原」的假設)互相矛盾。網上看到的英文版(Internet Archive版本)原文是 "your story leads to a contradiction",譯做「自相矛盾」屬超譯。
早前寫過《泛科學》轉載《大話題︰邏輯》一書的內容有問題(紫煙亭後來寫了較詳細的FB帖文指出更多問題),而《泛科學》轉載、同樣出自《大話題︰邏輯》的另一篇文章介紹數學哲學中的直覺主義(intuitionism),也顯示作者對其書寫的內容了解不深。
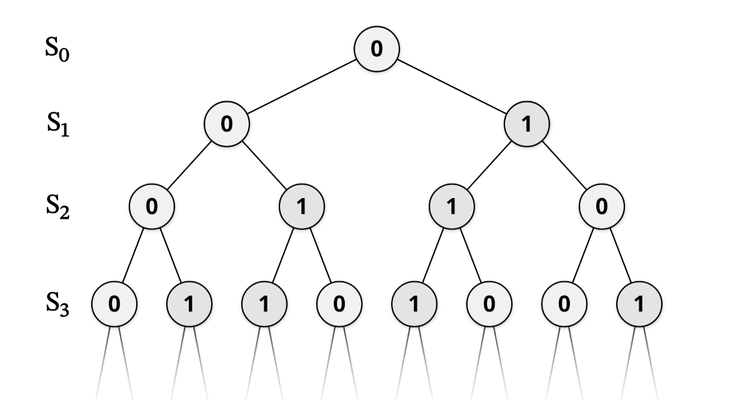
文章提到布勞威爾(L. E. J. Brouwer)反對在數學中無限制使用排中律,利用反證法指不能接受一個使用排中律的「惡魔論證」,因此結論為排中律不適用於無限集和無限序列。然而這短短一段(連同圖片)出現多個問題。
以下為有關段落截圖︰

不會出現「666」的無理數
按這段的脈絡理解,「666 這個序列一定會出現在任何無理數(如 π)的擴張裡」意思是任何無理數(假設使用10進制,下同)的小數部分一定會出現連續三個6。不過這句並不成立,例如以數學家劉維爾(Joseph Liouville)命名的劉維爾常數既是無理數,其小數部分又不可能出現「666」。
劉維爾常數的定義如下︰
$$ \sum^{\infty}_{k=1} \frac{1}{10^{k!}} = 0.1100010000000000000000000001000 \ldots $$
根據定義,當n是完全數時,劉維爾常數小數點後第n位是1,其餘為0。這個數字是超越數(transcendental number),自然也是無理數,而且明顯不可能在小數點後出現「666」 — — 別說連續三個6,一個也沒有。
雖然原文使用 “any irrational number like π” ¹,可譯為「像 π 一樣的無理數」,即使如此理解,作者也沒說清楚何謂「像 π 一樣」。
無法逐一檢查 ≠ 假
既然並非所有無理數都一定會出現「666」,讓我們收窄一點,以下僅討論 π 這個無理數。
這個「惡魔論證」指 π 的小數點後不會出現「666」這件事「數學上無法證明」,提出的「原因」居然是我們(人類)只能檢查有限個數字。然而如此排除以其他方法證明的可能,未免過份粗疏。要證明 √2 是無理數,即不可能把 √2 寫成兩個整數之比,我們不用檢查所有(整數為分子及分母的)分數。
退一步而論,就算假設︰
- 只有「把 π 算出來再檢查當中是否出現『666』」這個方法,而且
- 「666」不在 π 的小數點出現²
也僅代表「π 的小數點後數字不包含666」這句無法證明,而非像圖中那「惡魔」所言「這句陳述為假」(此處更假設了它屬實³),我無法理解這個「惡魔論證」如何「邏輯上能證明」 π 的小數點後會出現「666」。
我猜測這個「惡魔論證」的問題,源於作者誤解了直覺主義者(特別是布勞威爾)提出有關例子時的思路。
布勞威爾的例子
布勞威爾的確曾使用 π 作為例子,但跟上述「惡魔論證」的討論有別。在其1923年討論排中律的文章中,他透過 π 定義了一個實數 r,其數值取決於 π 小數點後是否出現「0123456789」以及首次出現的位置︰若首次出現在第 n 位則 r = (-½)ⁿ,否則 r = 0。
根據此定義,r 可能大於零(n 是偶數)、等於零(n 不存在)或小於零(n 是奇數),布勞威爾的直覺主義立場認為這三項均不成立(當時數學家尚未知道 π 小數點後會否出現「0123456789」),從而反對「< 為實數集的全序關係」此一說法。⁴
布勞威爾先反對排中律,再以上述例子說明數學中一些廣為接受的陳述(按其直覺主義立場)不成立。《大話題︰邏輯》的作者則反過來,聲稱布勞威爾不接受「惡魔論證」而推論排中律也不能接受,似乎誤讀了布勞威爾的例子(但我不肯定作者寫這一頁時參考甚麼文章/書籍)。
「666」及「0123456789」均在 π 中
事實上,「666」及「0123456789」均有出現在 π,除了呼應「惡魔論證」的「惡魔」外,我想不到《大話題︰邏輯》的作者為何要選「666」這串數字。
π 小數點後第2440位首次出現連續三個6,而在首10000位出現了6次「666」。⁵《美國數學學會通訊》(Notices of the AMS)的一篇文章則提到日本計算機科學家金田康正(Yasumasa Kanada)發現「0123456789」出現在 π 小數點後第 17,387,594,880 位,即近174億位。⁶
所以根據上文布勞威爾的定義,r > 0。
註︰
- 見Internet Archive上的英文版。
- 這假設本身錯誤(見下文),畢竟代表 π 並非正規數(normal number),數學家應該很快便能發現,關於正規數可參考我幾年前的文章。
- 其中一個問題是我們能否作出此假設,直覺主義者應較能接受「人類技術所能算出最精確的 π 的近似值不會出現連績三個6」這種表達方式。
- Brouwer (1923b, 1954, and 1954a). On the significance of the principle of excluded middle in mathematics, especially in function theory, Addenda and corrigenda, and Further addenda and corrigenda. 我參考的是 Jean van Heijenoort (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931,見第337頁。
- 我用 y-cruncher 計算 π 的值,猶他大學數學系的網頁亦列出 π 小數點後首10000位,不過每5個數字以空格分隔,在網頁搜尋「666」只找到其中兩組,須搜尋「6 66」才可找到其餘四組。
- 見文章第3頁,文中亦提到布勞威爾及希亭(Arend Heyting)等直覺主義者常以此作例子。我嘗試驗證但 y-cruncher 警告電腦記憶體不足(計算250億位需要 125 GB),連同虛擬記憶體也不夠。