我上過的集合論課

話說最近亂講物理、數學和哲學的林文欣到本人FB專頁吵鬧（有興趣可以看這則帖文下的留言），本來因為他提到而想寫點集合論的，但寫數學不用符號太麻煩（要是我不斷寫 \$x \in y\$ 甚麼的也不便大家閱讀），還是有空再算，寫點比較簡單的東西。

八年前我仍在布達佩斯讀碩士，我讀的是邏輯系，一位同學介紹我可選數學系的集合論課（他早我一年入學，已讀過這科，後來去讀博士也是研究集合論），自然不可錯過。

我住在校園附近，上學只是3分鐘路程，但數學系在另一個校園，需要到多瑙河的另一邊上課，冬天時比較需要意志，但未曾缺課。

教集合論的教授的Erdős number是1（畢竟是匈牙利的數學家），兩個學期的課程以一些large cardinals為主軸，由infinite combinatorics到forcing亦有觸及。

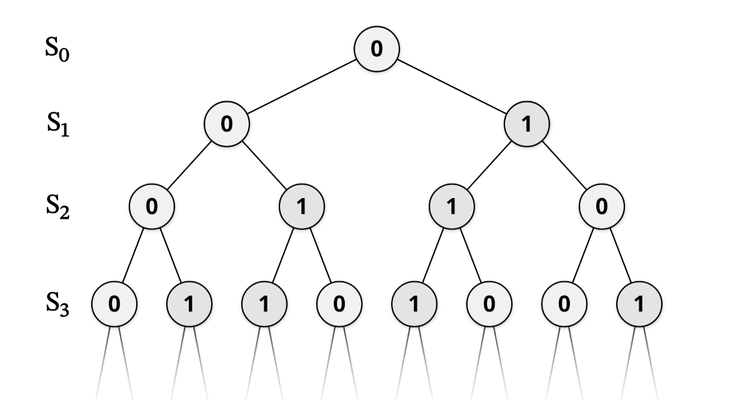
這樣寫好像只拋出一些名詞嚇人，我嘗試解釋一下︰集合論源於康托爾（Gerog Cantor）對無限的研究，特別是他以一一對應去比較兩個無限集是否相同「大小」、發現了無限可分為可數和不可數，以及可透過冪集（power set）構造更「大」的無限集。後來因為集合論出現悖論，迫使數學家轉向使用公理集合論（axiomatic set theory）如ZFC。

學習這些公理、康托爾定理（Cantor’s theorem）、無限可分為可數及不可數等等，都是一般集合論課程中非常基本的部分。（至於我上的集合論課，第一課時教授已在介紹measurable cardinals。）

所謂的large cardinals，就是一些更「大」的無限，大到ZFC本身也無法證明它們存在，只能假設它們存在去研究。而且這些無限強到足以證明ZFC一致，基於哥德爾不完備定理，我們也無法以ZFC證明這些large cardinals的存在跟ZFC一致。研究large cardinals主要是研究它們會帶來甚麼後果以及跟其他large cardinals的關係，其實頗為有趣，嚴格來說它們有可能不一致而只是尚未被證明。

Infinite combinatorics類似組合數學，但對象由有限的集合變成無限，主要是Ramsey theory，粗略來說是研究隨意劃分某些無限集時，有哪些特性必然存在。Forcing則是1963年由Paul Cohen創造的技巧，用來建立集合論的模型，當年他用來證明選擇公理（axiom of choice）和連續統假設（continuum hypothesis）跟ZF的公理獨立（ZFC就是ZF加上選擇公理）。

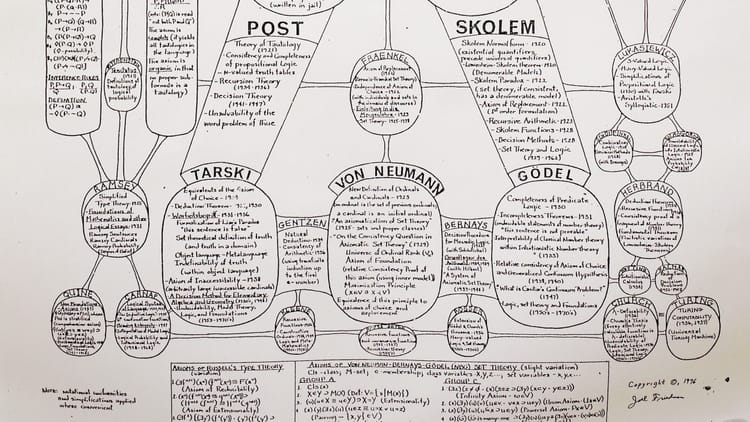
這些都是非常抽象的東西，不懂沒問題，但我想說的不是我很懂很多（一直沒用過自然忘記了大多數內容），而是這根本沒甚麼好炫耀的。在Thomas Jech的教科書（就叫做Set Theory）中，我讀的課題主要都是第一部分「Basic Set Theory」後段至第二部分「Advanced Set Theory」的內容（也沒有完全覆蓋），這本書還有第三部分「Selected Topics」。

然後見到林文欣這種人四處去問人「有人懂康托爾集合論中，無限可以比較大小？」，我甚至連嘲笑他的意欲都沒太多，只覺得可悲。

話說回來，雖說老師教的內容很多都忘了（真要讀回來也不是不可行，只是需要心力時間），我還記得第一個學期某天課前，其他同學未到，在圖中那個課室跟他閒聊，他知道我來自香港，跟我說他支持香港人。

（原刊於Medium）