隨機的規律

有線的《新聞刺針》訪問了《新報六合彩玄機》副總編輯林沖,這是一份提供六合彩「貼士」的報紙,據節目表示,坊間有七份這類彩報。
萬一馬會在六合彩攪珠做任何手腳,這類彩報自然沒有用——你應該去打探內幕消息,而非花幾元買一份彩報。因此以下先假設馬會沒有做手腳,亦有監察防止他人做手腳(這符合馬會利益,否則一但被揭發就會令投注額大減)。
節目提及以生肖、神仙以至卡巴拉去推測的方式,副總編指「哪個專欄看得最入腦,就可能跟你有緣」,我當然認為這是大包圍的技巧。如果我是神仙應該不想理會六合彩結果,以下亦假設神仙之類的東西(假如存在)不會影響結果。
現實中的攪珠不會是嚴格意義下的隨機事件,只要知道攪珠內的所有初始條件,理論上可以計算出攪珠結果,但除了計算本身複雜外,要得悉所有數據相信不太可能。
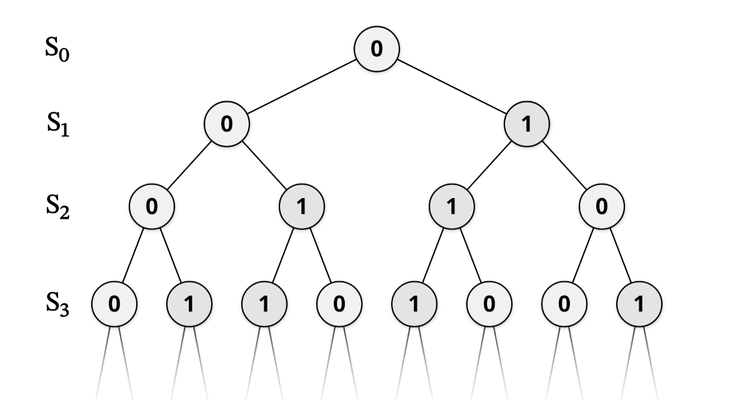
我們不妨再假設結果接近隨機攪出,這些彩報正是企圖透過結果歸納出一些規律或「玄機」。節目拍攝時,某次開彩結果中有三個數字跟上次結果相同,副總編就問︰「下一期又會不會出現很多重開的數字?」
人類是擅長尋找規律的動物,這項技能對我們的祖先生存有幫助,故在演化上有優勢。不過其「副作用」是我們有時會被誤導,在雜亂無章的訊息中看出意義和規律。
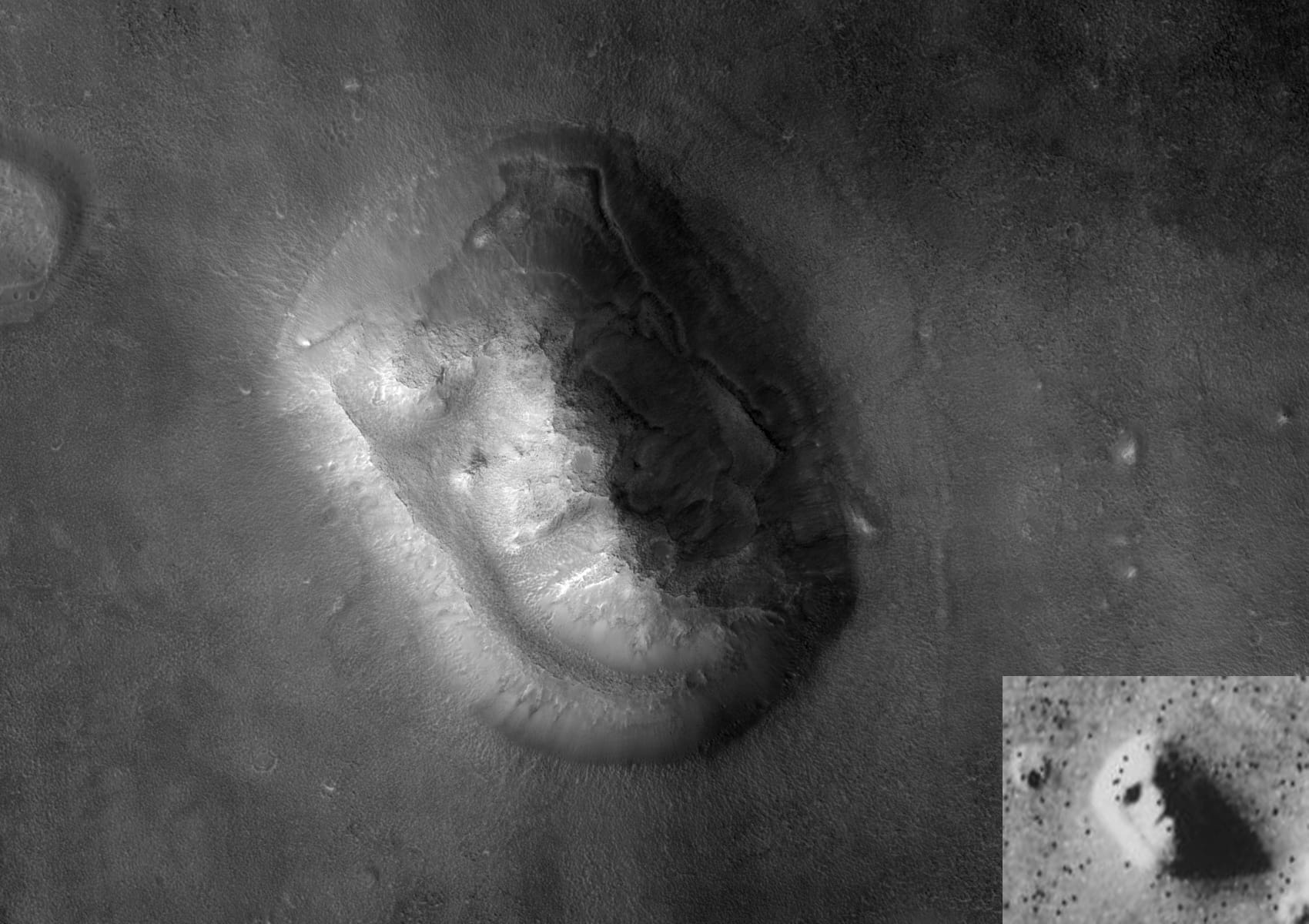
另一個類似例子是,人類辨認臉孔的能力,讓我們在一些痕跡中找到人臉,這類痕跡有時被認為是妖魔鬼怪作祟,有時被認為是神明聖人顯靈。
容我扯遠一點,數學中有個範疇叫做「藍斯理論」(Ramsey theory),以數學家、哲學家及經濟學家藍斯(Frank Ramsey,又譯作拉姆西)命名。
僅26歲就英年早逝的藍斯,在1928年一篇邏輯論文中證明了後世稱為「藍斯定理」的結果,這亦是藍斯理論的奠基石。在該論文中,藍斯定理只是一條小引理,他要解決的是一階邏輯判定問題(decision problem)的某個特例。
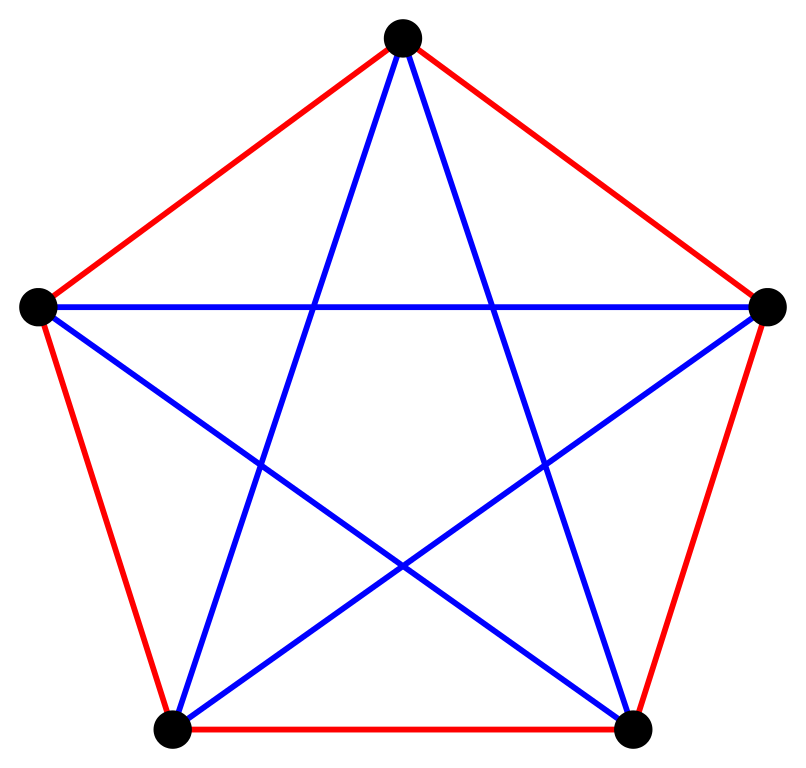
粗略來說,藍斯理論研究各種規律出現的條件。一個非常簡單、常用來介紹這理論的問題是︰最少要找多少人,才可以確保最少有三人互相認識或互不認識?(答案是六個人,證明詳見此文開首。)
藍斯理論通常以顏色去提出問題,例如︰若把一個(由頂點和邊組成的)圖形的邊隨意填上藍色和紅色,這個圖形要有多複雜才可以確保有一個淨色(純紅色或純藍色)的三角形?(這個問題就跟上一段的問題有關。)
說回像六合彩攪珠般的隨機事件,如果你不斷擲骰,總有機會在某些時刻擲出一些連續而有規律的結果,例如多次出現相同數字或者「123456」等(前提當然是骰子可以擲出1至6每個數字),只是你無法確定下一次會擲出甚麼結果、會否延續先前的機率。
數學家猜想圓周率π是「正規數」,即其小數位數字分佈中,任何有限數字串出現的頻率都跟其他相同長度的數字串一樣。這是個未經證明的猜想,不過多項統計測試均顯示π符合要求。即使如此,單看局部的話,我們仍然會看到感覺上較特別的數字串,例如在小數點後第762個位開始出現的「999999」,或者在第17387594880個位出現的「0123456789」。
我們的大腦很容易被迷惑,誤把巧合當成規律。倘若下一次開彩的結果出現其他現象,比方說有兩三個數字是上次開彩的數字加一,或者只有單數,那些彩報又會指出新的規律給讀者參考,然後忘掉上一期的發現。
相關文章︰



(原刊於Medium)