運算順序

近日Threads上出現關於乘法順序的討論,源頭應為一張圖片,顯示學生回答「7頭牛一共有幾隻腳?」時寫了「7×4=28」,被老師打上交叉並更正為「4×7=28」:

這類問題在網上每隔一段時間就會浮現,今次是「7×4」,幾個月前是「9×4」,去年也有「5x8」。反對更正學生的一方認為,基於乘法交換律(a×b=b×a),乘法的順序並不重要;支持更正的一方則認為須確保學生掌握乘法的概念,所以應規定按「正確」順序寫算式。
我的立場比較傾向前者,此問題重點在於乘法的本質而非順序,至少我們不知道學生寫「7×4=28」時,到底掌握了交換律、以另一方式點算,抑或單純搞錯了順序。如果希望學生掌握有關概念,要求寫清楚單位比規定順序有效。
有反駁引用網友舉例指演講費「5000元×1場」跟「5000場×1元」意思有別,但類比不當,畢竟寫「5000元/場×1場」跟「1場×5000元/場」意思都一樣,也不會引起誤解。有人則貼出教科書說明乘法定義,表示乘法算式應寫成「被乘數×乘數」:
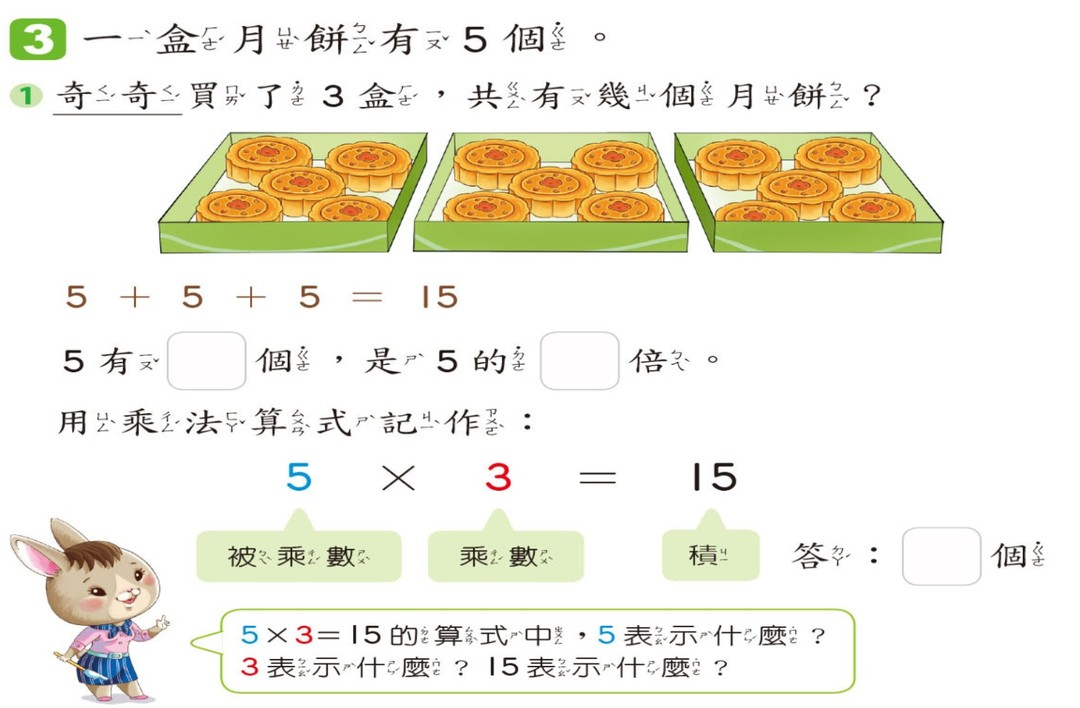
然而「乘數」和「被乘數」的順序定義任意(arbitrary),倒轉過來亦無不可,掌握乘法概念的重點不在於算式是否「順序」。
另外有人說「數學公理中根本沒有定義乘數、被乘數的觀念」,這說法不準確,因為乘法本身定義為重複的加法,相加的次數就是乘數、被加的數字就是被乘數。
在皮亞諾算術公理(Peano Axioms)中,涉及乘法的兩條公理如下(為方便起見,先假設讀者了解加法、0以及「+1」的定義):
- $ m \times 0 = 0 $
- $ m \times (n+1) = m \times n + m $
此處的乘法用上遞歸定義(recursive definition),雖然沒有直接對每一組「$m \times n$」下定義,但我們可以根據該兩條公理計算出每一組「$m \times n$」。例如:
$ 2 \times 2 = 2 \times 1 + 2 = (2 \times 0 + 2)+2 = 0+2+2 $
(嚴格而言,皮亞諾算術中的數字只有$0$,其他數字透過不斷使用後繼函數$S(n)$去表示,例如$1=S(0)$、$2=S(S(0))$,惟非此處重點。)
所以根據這兩條公理,乘法的順序就是「被乘數×乘數」。不過這兩條公理中乘法的順序並無任何特別之處,我們可使用以下公理代替:
- $ 0 \times m = 0 $
- $ (n+1) \times m = m + n \times m $
在這個系統乘法的順序則是「乘數×被乘數」,然而實際上沒有任何影響,只要連同其他公理,一樣可推導出乘法的交換律。
順帶一提,首個提出以此方式定義乘法的數學家並非皮亞諾(Giuseppe Peano),而是格拉斯曼(Hermann Grassmann),他在其著作 Lehrbuch der Arithmetik(Textbook of Arithmetic)中使用此定義。根據《Roads to Infinity》第135頁的說法,格拉斯曼是高中老師,寫這本書原打算用作課本,希望不會有人因為堅持學生掌握乘法概念而要學校教授皮亞諾公理。
另一個在網絡上不時浮現、同樣跟運算順序有關的問題是「6÷2(1+2)」,隨便搜尋即可見到有媒體於2019、2020甚至2024年「報導」(這類翻炒網絡話題的文章難以稱得上是新聞報導,而且引用資料通常錯漏百出,例如所謂的「美國史丹福大學教授塔沃克」其實是在該大學讀經濟及數學)。
此問題的爭論在於應該計算「(6÷2)×(1+2)」抑或「6÷(2×(1+2))」,前者為9後者為1。不同計數機採取不同解讀,就得出不同答案。

嚴格來說,「6÷2(1+2)」本身寫得不夠清晰。平時為免寫那麼多括號,我們會規定「先乘除,後加減」去避免歧義,例如「5×2+3」就代表「(5×2)+3」,如果想寫「5×(2+3)」就只能完整寫出括號。至於「6÷2(1+2)」即「6÷2×(1+2)」,在「先乘除,後加減」下,乘法和除法並無先後之分,只需要按順序計算,所以答案應為9。
這條問題引起爭論的原因,相信是「2(1+2)」的寫法比較像代數中有時略去乘號的寫法而被解讀成「(2×(1+2))」,例如「3/2x」我傾向會解讀為「3/(2x)」而非「(3/2)×x」,因為後者可以寫成「3x/2」。然而如此解讀的話,「先乘除,後加減」這條規則就不夠精細,需要再額外區分「用括號表示的乘法」,弄得那麼複雜,似乎違反了有關規則簡化寫法的原意。無論如何,完整寫出算式便沒有問題。
如果想不寫括號,又不引起誤會,我們可以使用「波蘭記號法」(Polish notation):先寫運算符號(如+-×÷),再寫相應的項(數字或其他算式)。
例如算式「5×3」以波蘭記號法書寫就是「× 5 3」,「5×(3+1)」則是「× 5 + 3 1」。解讀算式時由左至右看,由於只有「運算符號 數字 數字」的排列才可計算,毋須括號也能區分運算順序。套回「6÷2(1+2)」的例子,以波蘭記號法書寫「(6÷2)×(1+2)」就是「× ÷ 6 2 + 1 2」,「6÷(2×(1+2))」則是「÷ 6 × 2 + 1 2」,不會引起混淆。
波蘭記號法不僅適用於四則運算的算式,任何二元運算都可適用。雖然看起來簡潔,但我猜大多數人寧願保留括號。