也談連續統假設

幾個星期前看到這篇文章︰

但因為香港近來的狀況,現在才有空寫點東西。
先指出文中幾個問題︰
- 那個「牽手關係」其實不是單純的「函數」,而是「單射函數」(injective function),既然都用上術語就說清楚比較好。
- 順道一題 >> 順道一提(順道抓個別字)。
- 對角線證明那一段,第三步其實應該註明要怎樣「不一樣」,才能避免得出 0.29999999… 之類的數字,因為這可能跟表上另一數字(即 0.300000…)一樣,無法推論出矛盾(但這有點技術性,只是需要注意一下)。
- 哥德爾和 Cohen 那兩個結果需要假設 ZF 本身一致(即沒有隱含矛盾),否則你可以用 ZF 證明任何東西,自然包括證明連續統假設及其否定。
- 文中指「他們只說,任何人都沒有辦法透過從公理系統開始的一系列推論,去證明連續統假設是對的還是錯的。」其實哥德爾和 Cohen 沒有這樣說,他們的證明只適用於 ZF 這個系統(和類似系統),畢竟可以把連續統假設列為公理,這樣就很容易「證明」。
- 文中指「它終究有個對錯,老天知道,但老天沒有給我們推論出真相的可能性。」它(連續統假設)終究有沒有對錯呢?這其實是個數學哲學問題,不要那麼輕易斷言,首先要說清楚如何界定對錯,之後那句「它有個對錯,但你證不出來」有相同問題。
- 文中指「聽起來超弔詭的,但即使在數學裡面,還是有這種介於對錯之間的東西。」連續統假設不是「介於對錯之間」,只是獨立於 ZF 的公理。
連續統假設(Continuum Hypothesis, CH)是推動集合論發展的重要問題,由哥德爾證明它跟 ZF 一致,到Paul Cohen證明它的否定跟 ZF 一致,都帶來集合論的新技巧,其中 Cohen 的 forcing 更為集合論帶來大量新發現。
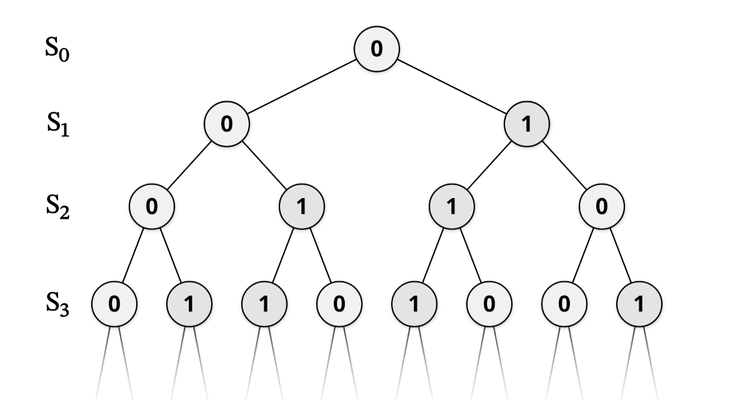
簡單而言,可以把公理系統——例如集合論常用的 ZFC(那個C指選擇公理,同樣獨立於 ZF,而 CH 亦獨立於 ZFC,所以以下都用 ZFC)——理解成一串按規則轉換的符號,而每套一致的集合論公理都有其模型(model),哥德爾和 Cohen 做的,其實是為 ZFC 建立不同模型,前者建立一個 CH 成立的模型,後者則建立一個 CH 不成立的模型,兩個模型都符合 ZFC 的公理,因此如果 ZFC 是一致的話,就不可能證明或否證 CH。
CH 成立的情況其實比較簡單,就是「可數無限」與「連續統」之間沒有其他無限。但 CH 不成立的話,我們就要問「可數無限」與「連續統」之間到底還有甚麼無限——數學家發現,幾乎你想「僭建」多少個無限進去兩個無限之間都可以,又或者說,你想連續統多大,總能建立一個相應的集合論模型(還是有點限制,但太技術性,我不打算在這兒談)。
值得一提的是,集合論中有個分支專門研究「大基數」(large cardinals)——「大」到 ZFC 也不可能證明其存在的無限——通常都是假設某種無限大存在,再研究能夠推論出甚麼結果、跟其他無限大的關係如何之類(所以嚴格而言其非研究那些基數,而是假設其存在的命題)。有趣的是這些假設似乎有種層級關係,通常都是假設某種無限大存在,就能夠推論出另一種無限大存在(也有例外),而 CH 卻跟所有假設互相獨立,沒有一個大基數強到其存在可蘊函 CH。
到底會不會某天有人發現一條大家都接受的公理,結合 ZFC 後可以證明(或否證)CH?理論上當然有可能(我不太相信),萬一真的有這麼一天,而且這條新公理廣為數學界接受,成為主流公理之一,那時候大家都會認為 CH 是真的了——不過這情況應不太可能發生。
另一個可能是,CH 可以推論出一些對數學界非常有用甚至無法摒棄的結果,令數學界決定接受 CH 作為集合論公理——當然機會也是甚微。不過選擇公理正因為類似的理由,才成為主流接受的公理(所以常用的集合論是 ZFC)。在 ZF 中無法證明或否證選擇公理,但這件事本身沒甚麼弔詭的,選擇公理也不是「介於對錯之間」。
延伸閱讀︰