未睇嘅書︰Computability and Unsolvability

📕 Computability and Unsolvability｜Martin Davis

序言二手書櫃買到嘅好嘢，邏輯學家Martin Davis第一本書，Dover平裝版本。

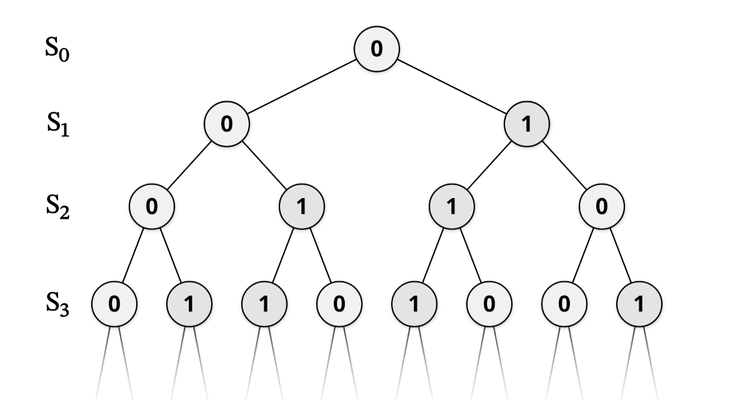
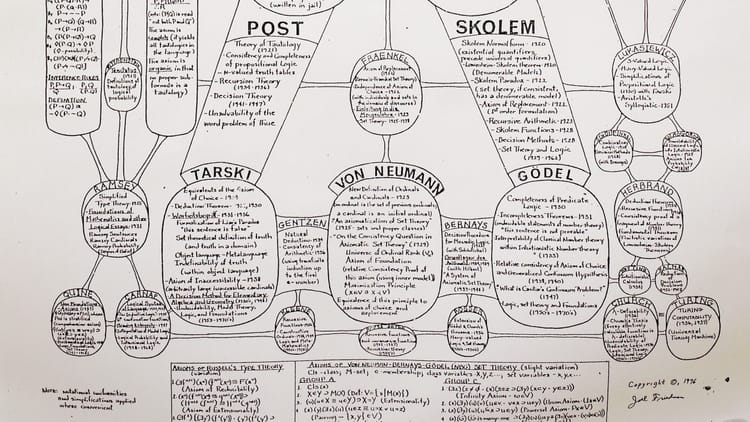
呢本係入門書（但都要有返咁上下底先睇得），介紹數理邏輯入面一個叫做「可計算性理論」（computability theory，早期又叫遞歸論 recursion theory）嘅分支。簡單嚟講，呢個學科源於研究乜嘢問題可以透過計算搵到答案，係電腦科學嘅基礎。當時啲數學家、邏輯學家同哲學家嘗試為數學搵個可靠基礙，結果就令到電腦誕生。呢科入面最出名嗰位應該就係圖靈（Alan Turing）。

喺搵咩可以計到答案嘅過程中，佢哋又發現有啲問題係無法解決，其中一個係Davis有份研究嘅「希爾伯特第10問題」（Hilbert's tenth problem）。呢個問題係問有無可能搵到個演算法，可以判斷任何「丟番圖方程」（Diophantine equation）有無整數解。而「丟番圖方程」其實只係由多項式構成嘅方程式，其中要求所有系數（coefficient）都係整數，例如x+y=10、x²+1=0等等——前者有整數解（仲有無限多個），後者無。

最終 Yuri Matiyasevich 嘅發現結合埋 Julia Robinson、Martin Davis 以及 Hilary Putnam（就係嗰位哲學家）之前嘅結果，證明咗「希爾伯特第10問題」無解。換言之，唔存在一個演算法可以畀你入條「丟番圖方程」入去，就話你知條方程式有無整數解。呢條定理就叫做MRDP theorem。

其實呢本書我都唔係完全無睇過，事關書入面有個附錄就係證明MRDP theorem，之前有次諗開某個關於哥德爾不完備定理同悖論嘅問題，需要了解下個證明方法所以望過下個附錄。

今次揭返先發現當時攝咗張《大象席地而坐》嘅戲飛，所以係2019年1月26日後睇，斷估都係上半年睇，下半年無呢個精神時間（嗰陣好似只係斷斷續續咁睇咗 Susan Haack 本 Philosophy of Logics）。

《大象席地而坐》套戲成四粒鐘，但睇嗰陣唔覺過咗咁耐，只係記得睇完好壓抑，可惜係導演胡波首作兼遺作。嗰個周末仲睇埋《牯嶺街少年殺人事件》（又四粒鐘）同《一一》（三粒鐘），夾埋睇咗成11個鐘戲。

P.S. Dover啲數學書都幾多好嘢，又平，但早幾年先知某外籍高級紀律部隊人員個姓原來都係Dover，即刻有啲唔開心（好在叫開中文名，無聯想埋一齊）。

（原刊於Instagram）