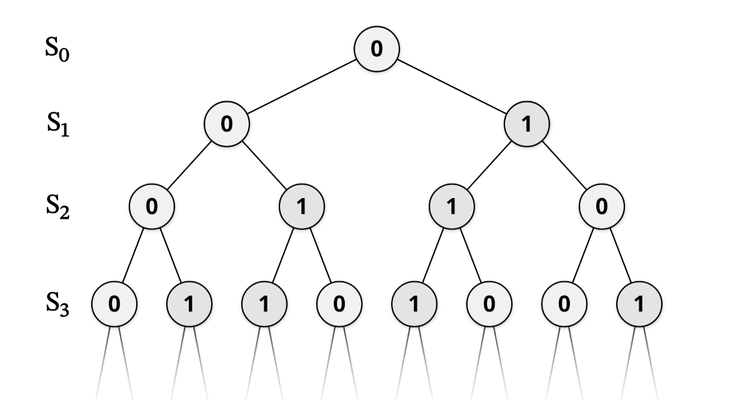
填色問題的上/下限與有/無限
數學家 Edward Nelson 仍是大學生的時候,想到以下問題︰如果要把平面填滿顏色,同時沒有相距一個單位(甚麼單位不重要)的兩點有相同顏色的話,最少要多少種顏色?
在提出這問題不久後,Nelson 及其友人已知道這個數字——稱為「平面色數」(chromatic number of the plane, CNP)——範圍在4至7之間(填滿一個圖所需的最少顏色數目,稱為該圖的「色數」)。六十多年來,雖然問題獲數學界關注,但答案仍然未有進展。
這個問題亦可以圖論語言表達︰若G是一個任意的無限等距圖——即所有相鄰(由同一條邊連接)的頂點相距剛好是一個單位(也可理解為這個圖由長度為一單位的邊組成)——要把G的頂點填色,並確保相鄰兩點不同色,最少要多少顏色?
直到今年4月,一位業餘數學家 Aubrey de Grey 構造了一個須用最少5種顏色填滿的等距圖,帶來突破。關於為何答案要在4至7之間、de Grey 的構作方式等內容,可參考我寫的文章︰

此處我想討論這個問題中無限和有限之間的關係。
Nelson 問題涉及無限等距圖,要提升 CNP 下限,只需要構作需要更多顏色來填滿頂點的有限等距圖(例如 de Grey 的圖需要5種顏色),因為我們能夠把有限等距圖擴展成無限等距圖。
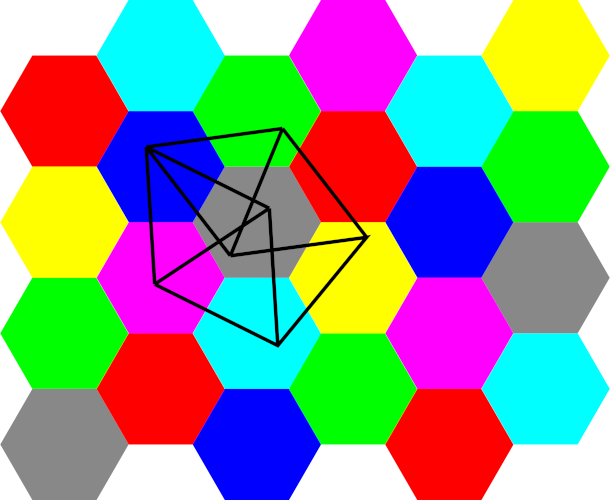
假設有數學家構造出需要色數為7的等距圖,那就一切好辦,我們知道 CNP = 7。萬一 CNP 原來是 5/6 的話,數學界需要把 CNP 上限降低,這就沒那麼容易了。現時 CNP 的上限源自下圖(證明詳見上述連結)︰
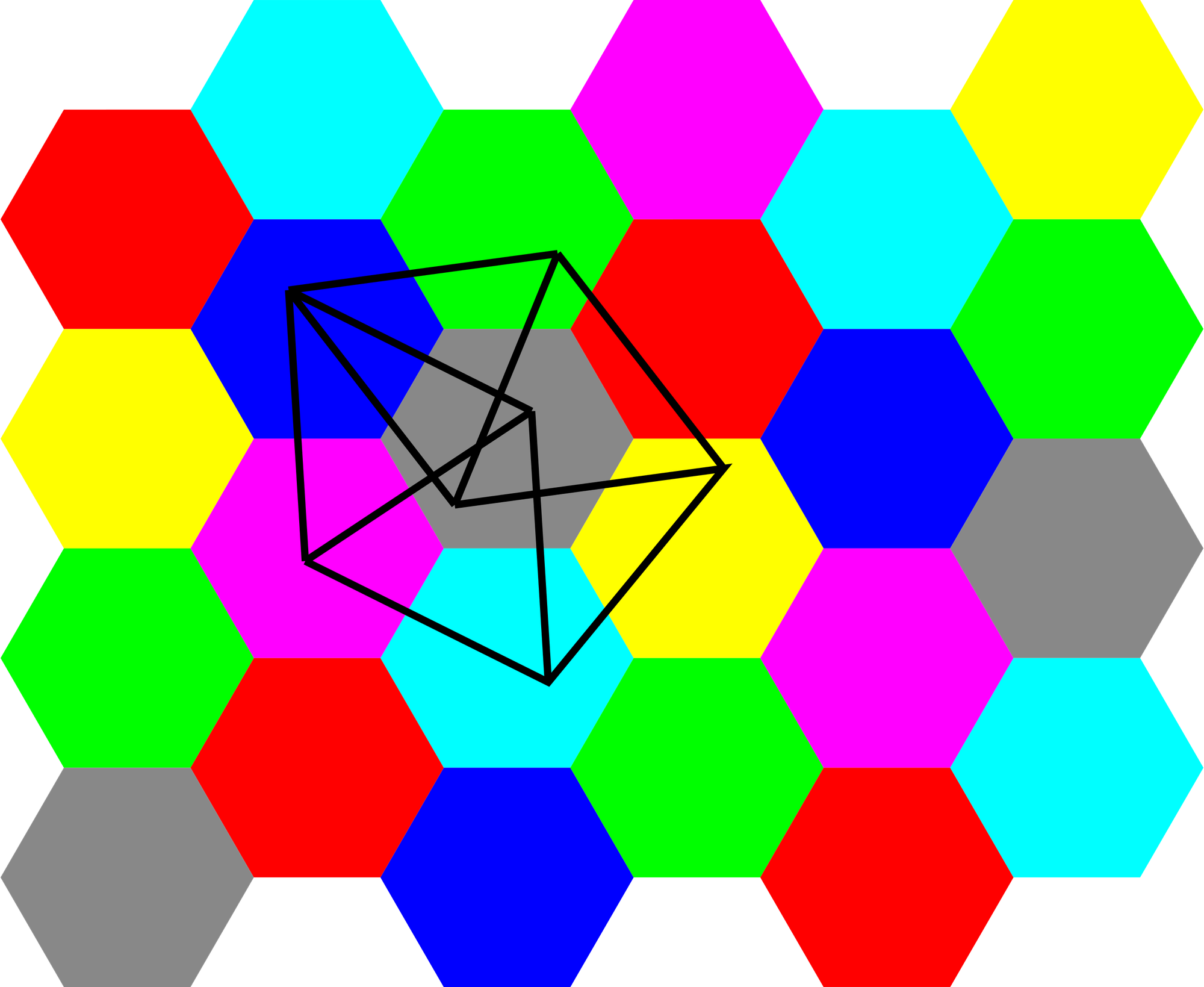
一個用6種顏色便可填滿平面的圖案,能夠把 CNP 下限降低(如果是5種的話更能直接解決問題),不過既然那麼多年來都沒有人想到,我猜並不容易。
另一個問題是,無限和有限之間會不會隔着一道鴻溝,以致——比方說——所有有限等距圖都只需要5種顏色來填滿,而有些無限等距圖卻需要6種?
Nicolaas Govert de Bruijn 及 Paul Erdős 在 1951 年證明的定理告訴我們不會如此。這條定理說的是,假如一個無限圖可以用有限種顏色填滿,其色數就等如該圖的有限子圖(subgraph)的色數中最大那個數字。
由於 CNP 上限是7,肯定是個有限數字,De Bruijn–Erdős 定理確保了,萬一 CNP=6 的話,必然存在一個色數為6的有限等距圖——能不能找到是另一回事。
然而這條定理需要用到選擇公理(axiom of choice)去證明,在選擇公理不成立的集合論模型中,有限等距圖和無限等距圖之間還是有可能存在那道鴻溝。
我想以一個令我大開眼界的發現作結。在寫 de Grey 那宗新聞時,我讀了一點 Alexander Soifer 的 The Mathematical Coloring Book。在寫這篇文時又讀多一點,發現 Soifer 跟集合論專家 Saharon Shelah 在 2003年證明了,存在一個(頗簡單的)圖G,其色數在選擇公理成立的 ZFC 內為2,而在選擇公理不成立——但可數版本的選擇公理成立,以及所有實數集 Lebesgue 可測 ——的 ZF 集合論中卻不可數︰